Как найти стороны прямоугольника, если известна площадь и периметр?

Если периметр прямоугольника Р = 30 см, а его площадь S = 56 см, то его стороны будут равны :

а - одна сторона, в - другая сторона прямоугольника.

S = а * в

P = 2а + 2в

Решив эту систему, приходим к тому, что сторона а будет равна 7 см, а сторона в будет равна 8 см.

а = 7 см в = 8 см.

Можно попробовать решить данную задачу, составив систему уравнений.

Периметр прямоугольника равен: p=2a+2b;

Площадь прямоугольника равна: s=a*b;

Так как мы знаем периметр и площадь, то сразу подставляем числа:

30=2a+2b;

56=a*b;

Выражаем b через a во втором уравнении:

b=56/a;

И подставляем 56/a вместо b в первое уравнение:

30=2a+2(56/a);

15=a+56/a;

Домножаем обе части на a:

15a=a?+56;

Получаем квадратное уравнение:

a?-15a+56=0;

Находим корни этого квадратного уравнения:

(15±v(15?-4*1*56))/2*1 = (15±v(225-224))/2 = (15±v1)/2 = (15±1)/2

Получилось, что корни этого уравнения:

a1=(15+1)/2=16/2=8;

a2=(15-1)/2=14/2=7;

Получается, что у нас 2 возможных варианта прямоугольников.

Вспомним, что мы выразили: b=56/a;

Отсюда находим возможные b:

b1=56/a1=56/8=7;

b2=56/a2=56/7=8;

Как оказалось эти два разных прямоугольника - это один и тот же, просто достигнуть периметра в 30 при площади в 56 можно:

Если a=7 и b=8.

Либо наоборот: a=8 и b=7.

То есть в сущности у нас один и тот же прямоугольник, просто в одном варианте вертикальная сторона больше горизонтальной, а в другом наоборот - горизонтальная больше вертикальной.

Ответ: одна сторона 7 сантиметров, а вторая 8 сантиметров.

Чтобы решить поставленную задачу, нужно составить систему уравнений и решить ее

S = а*b

P = 2(а+b)

получим квадратное уравнение, которое легко решается, если подставить в него значения периметра и площади

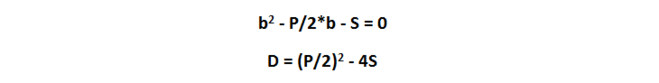
Дискриминант равен 1 и уравнение имеет два корня 7 и 8, следовательно одна из сторон равна 7 см, другая 8 см или наоборот.

Я специально выписал здесь дискриминант, так как по нему очень хорошо ориентироваться

если в условии задачи на нахождение сторон прямоугольника значение периметра и площади заданы так, что этот дискриминант больше ноля, тогда мы имеем прямоугольник;

если дискриминант равен нолю - тогда имеем квадрат (P=30, S=56,25, квадрат со стороной 7,5);

если дискриминант меньше ноля, то тогда такой прямоугольник не существует (P=20, S=56 - решения нет)

Дано: S = 56 см

Р = 30 см

Стороны=?

Решение:

Пусть стороны прямоугольника a и b.

Тогда: площадь S = a * b , периметр Р=2*(a + b),

Получим систему уравнений:

{a*b=56 ? {ab=56

{2(a+b)=30, {a+b=15 ,выражая b через а получим квадратное уравнение:

b=15-a, a^2 -15a +56 =0 ,решая которое ,получим :

a1=7, a2=8,

b1=8, b2=7. То есть стороны прямоугольника: a=7,b=8 ,или наоборот:a=8,b=7.

Нашла еще такое решение,

Известно, что периметр прямоугольника 30 а площадь 56, далее:

периметр = 2*(длина + ширина) или 2L + 2W

площадь= длина * ширина или L * W

2L + 2W = 30 (делим обе части на 2)

L + W = 15

L * W = 56

L * (15 - L) = 56

Честно говоря, не совсем поняла решение, но думаю, тот, кто не совсем подзабыл математику, разберется.

Вспоминаем школьную геометрию:

Периметр прямоугольника - это будет сумма длин всех сторон, а площадь прямоугольника - это уже произведение двух смежных его сторон (длину на ширину).

В данном случае нам известны и Площадь и Периметр прямоугольника. Они равны 56 см^2 и 30 см соответственно.

Итак, решение:

S - площадь = а x b;

56 = a x b;

Р - периметр = а + b + a + b = 2a + 2b;

30 = 2 (а + b);

15 = a + b;

a = 15 - b;

Делаем подставление:

56 = (15 - b) x b;

56 = 15 b - b^2;

b^2 - 15b + 56 = 0.

Получили квадратное уравнение, решая которое получаем: b1 = 8, b2 = 7.

Находим и другую сторону прямоугольника:

a1 = 15 - 8 = 7;

a2 = 15 - 7 = 8.

Ответ: стороны прямоугольника равны 8 и 7 см или же 7 и 8 см.

Зная формулы периметра прямоугольника и его площади, стороны ищутся в виде решения системы двух уравнений. Для начала выражаем значение одной стороны через другую и например площадь. Это выглядит так А=S/В=56/В

Затем подставляем это выражение вместо буквы А в уравнении для периметра:

Р=2(56/В + В)=30

Получаем что 56/В+В=15

В этом уравнении даже решать его не надо - любому человеку знакомому с таблицей умножения сразу видно, что 56 это произведение 7 и 8, а поскольку и сумма этих цифр как раз 15, то они и есть нужные нам значения сторон прямоугольника.

Обозначим одну сторону буквой Х, другую - буквой Y.

Площадь прямоугольника вычисляется умножением длин сторон, следовательно, мы можем составить первое уравнение:

Х*Y=56

Периметр - это сумма длин сторон, следовательно, второе уравнение такое:

2Х+2Y=30

Получаем систему двух уравнений.

По первому уравнению выделяем Х: Х=56:Y, подставляем это во второе уравнение:

2*56:Y+2Y=30 Отсюда уже легко найти значение Y: Y=7, тогда Х=8.

Периметр 30, площадь 56. Назовем стороны прямоугольника а и с. Тогда можем составить такие уравнения:

(а+c)х2=30

ахс=56

Далее решаем систему уравнений и находим, что стороны прямоугольника составляют 7 и 8 см.

Итак, для начала рассмотрим формулы для нахождения площади и периметра:

1) S = a * b = 56 см2;

2) Р = 2а + 2b = 30 см.

Ведь мы знаем, что прямоугольник имеет по две одинаковых стороны.

Таким образом нам требуется решить систему из двух уравнений:

a * b = 56

2а + 2b = 30

Отсюда получаем, что одна сторона равна 7, а другая 8.